SLAM

Nov 24 2021

The objective of SLAM is to estimate a robot’s state (position and orientation) and create a map of the robot’s surroundings simultaneously using the knowledge of its controls and the observations made by its sensors.

Introduction

The term SLAM is an acronym for “Simultaneous Localization and Mapping”.

Localization: Localization refers to the robot's ability to estimate its own position and orientation with respect to its surroundings. This is done by combining the robot's controls along with the data obtained from its sensors.

Mapping: Creating a map of the robot’s surroundings using its estimate on its position and the data obtained from various sensors.

SLAM aims to do both of these tasks simultaneously, using one to help improve its estimate of the other. This may not sound possible, but there are various algorithms like Kalman filter, Particle filter, and GraphSLAM that help provide an approximate solution in certain environments to both these problems.

The general idea of slam can be subdivided into different stages:

Landmark Extraction
Data Association
State Estimation
State Update
Landmark Update

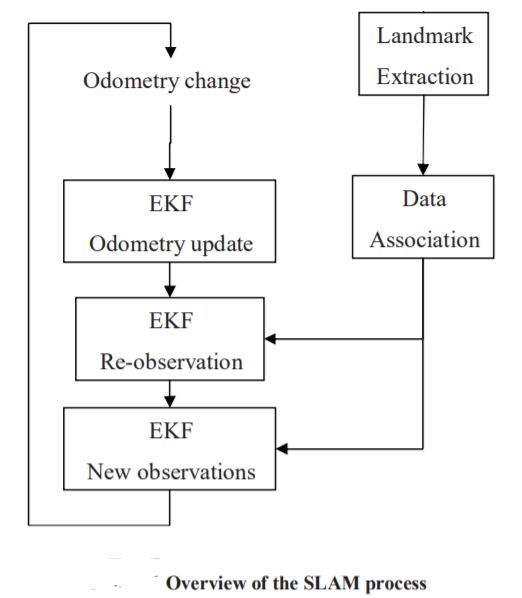
*In the image above, EKF stands for Extended Kalman Filter, an algorithm used for implementing SLAM.

SLAM is an idea through which we estimate the robot’s state through its controls, and using the locations of the landmarks we witness, we improve the estimate of the robot's state. It is based on a probabilistic model, where each item has a probability of being in a particular position.

Applications of SLAM

SLAM is used extensively in various indoor, outdoor, aerial, underwater and underground applications for both manned and unmanned vehicles.

For e.g. Reef monitoring, exploration of mines, surveillance drones, terrain mapping etc.

Probabilistic Interpretation of SLAM

In the probabilistic world, each measurement and estimate has some error associated with it, and we can only determine a probability distribution to estimate the map and localisation of a robot using SLAM. Mathematically, it can be represented as:

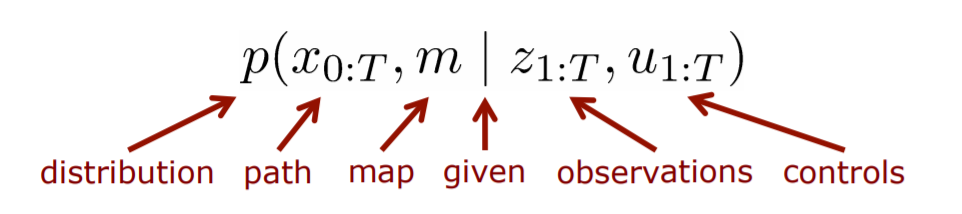
This means that the objective of SLAM is to obtain the probability distribution of the robot’s path and a map of its surroundings using the knowledge of the robot’s controls and the observations it makes using its sensors.

Below is a graphical representation of SLAM. xt is the location of the robot at time t, m represents the map, ut represents the controls of the robot at time t, and zt represents the values observed by the sensors on the robot.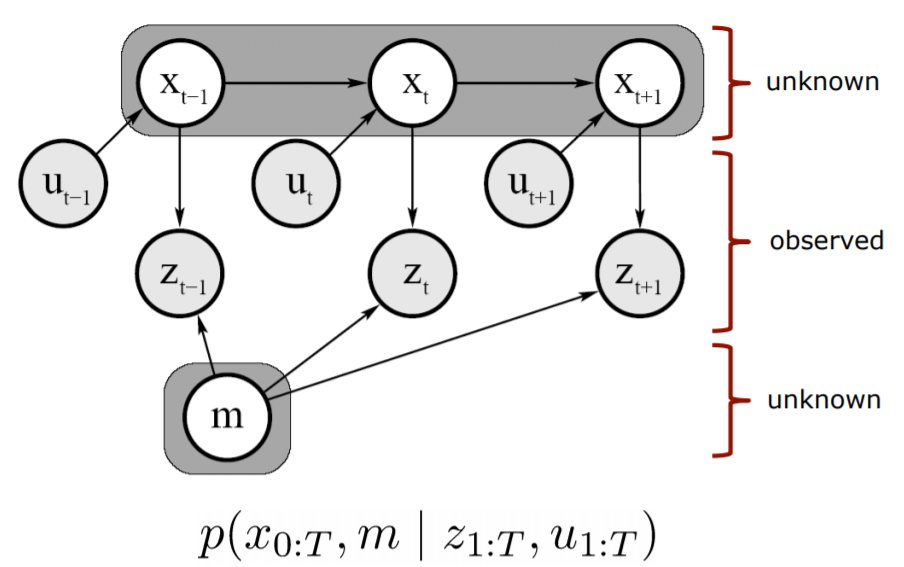

Homogeneous Coordinates

In SLAM, cameras are often used as sensors to obtain information about the robot's surroundings. Cameras don’t capture a 3D image, rather they capture a projection of the 3D world. The mathematical formulations can become simpler if we use projective geometry instead of euclidean geometry. The system of coordinates used in projective geometry is called homogeneous coordinates. The details regarding the mathematics of homogeneous coordinates can be found here.

Bayes Filter

A lot of the different models used for SLAM such as the Kalman Filter and the Particle Filter are based on the Recursive Bayes Filter. In the Bayes filter, the belief of xt is defined as

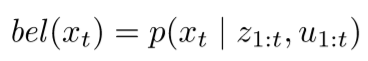
The recursive Bayes Filter can then be defined as a 2 step process:

Prediction Step
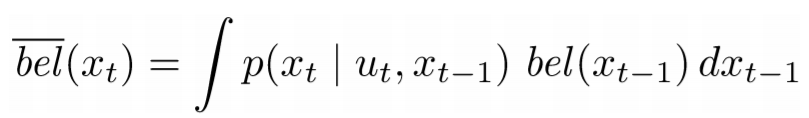
Correction Step

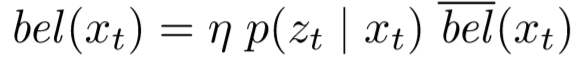
p(xt | ut, xt-1) represents the motion based model, which is the distribution of the current location based on the robot’s controls and its previous location. p(zt | xt) represents the correction introduced based on the sensor readings zt. This Bayes filter acts as a framework for different realizations such as the Kalman Filter and the Particle Filter. For further details regarding the Bayes Filter, refer here.

Motion Models

In the section of Bayes Filter, we saw the term p(xt | ut , xt-1) represents the motion based model. In general, there are 2 common types of motion based models:

Odometry based model
Velocity based model

The Odometry based model is mainly used for those robots that have wheel encoders, i.e. where it is feasible to count wheel motions and find the direction of motion. The Velocity based model is normally used where the odometry based model cannot be implemented, e.g. a drone does not have wheels and wheel encoders cannot be used. For a detailed description of the 2 models here including their mathematical formulations, check this document.

Sensor Models

The term p(zt | xt ) represents the sensor based model. It represents the probability distribution of getting a measurement zt at a position xt . There can be different kinds of sensors used.

Internal sensors such as gyroscopes, accelerometers etc
Proximity sensors such as Sonar, Radar etc.
Visual Sensors like cameras
Satellite based sensors like GPS

For more details regarding the Sensor Models, refer to this document.

Filters

There are 2 main methods used for implementing SLAM, that is the Kalman Filter and the Particle Filter. They are based on the Bayes Filter and use the motion and sensor models to get a good estimate for SLAM.

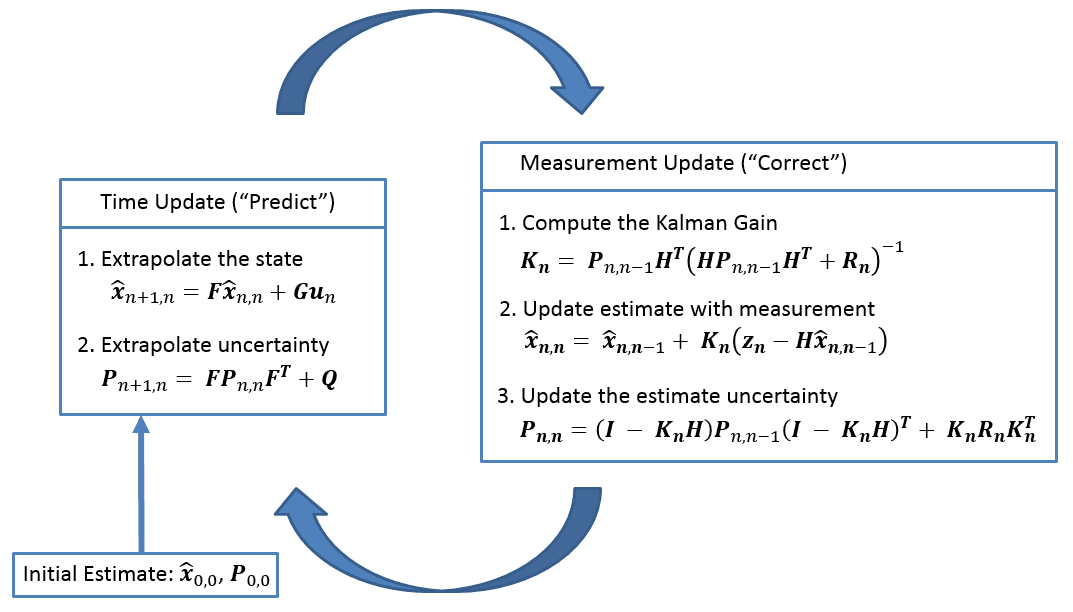
The Kalman Filter

The Kalman filter is a filter based on the Bayes filter, and is the optimal solution for the linear Gaussian case. It assumes all probability distributions are gaussian. For a complete tutorial on Kalman filter, check here. In short, the Kalman filter can be depicted as follows:

Particle Filter

The particle filter is also based on the Bayes filter, but it is superior to the Kalman filter in non-linear and non-Gaussian systems. The particle filter models by samples, and the more samples, the better the distribution.

For more details regarding the particle filter, check here or here.